GoMim AI | Learn Algebra Easily with Algebra Calculator

Algebra is one of the core branches of mathematics, providing the foundation for solving problems with symbols, equations, and patterns. From whole numbers and fractions and mixed numbers to more advanced topics like polynomials and rational functions, algebra creates the language that connects simple arithmetic to higher-level concepts. Whether you are starting with Algebra 1 or building a complete Algebra learning path, having the right tools can make a huge difference. An algebra calculator supported by the powerful AI Math Solver feature in GoMim—alongside other capabilities like step-by-step guidance and multi-language support—serves as both an AI Homework Helper and an AI Math Calculator, helping learners simplify expressions, explore domain and range, and master topics step by step. This article will introduce the essentials of algebra while showing how modern Math AI tools can make the subject accessible, accurate, and engaging for all learners.

What is Algebra?

Algebra is a central branch of mathematics that uses symbols and letters to represent numbers and quantities within formulas and equations. These symbols can stand for known or unknown values, and algebra provides a systematic way to simplify relationships and solve for variables. From whole numbers and decimals to more advanced forms like polynomials and rational functions, algebra builds the framework that connects arithmetic to higher-level concepts.

For instance, in the equation x+3=5, algebra helps us determine the value of x, the unknown variable. With the support of an algebra calculator, learners can practice solving such problems more efficiently while exploring the logic behind each step, making the subject both approachable and practical.

Why Algebra Matters in Learning and Life

Algebra is essential because it acts as the gateway to advanced mathematics and practical problem-solving. It forms the basis for exploring calculus, geometry, and statistics, and it provides the tools needed to analyze the domain and range of functions, a skill that underpins both mathematics and science. Beyond the classroom, algebra is applied in engineering, computer science, economics, and even everyday tasks like calculating percent, working with ratio and proportion, or interpreting data written in scientific notation. For students preparing for exams such as the SAT or GRE, a strong command of algebra is non-negotiable. By practicing with an algebra calculator, learners can simplify complex problems, reinforce key concepts, and build confidence in tackling both academic and real-world challenges.

The Algebra Learning Path in U.S. Education

In the United States, algebra is introduced step by step, allowing students to gradually move from basic arithmetic toward higher-level mathematical reasoning. This algebra learning path ensures learners gain both procedural fluency and conceptual understanding. Throughout the journey, tools like an algebra calculator and a reliable AI Math Solver such as GoMim can provide extra support, making each stage more approachable and interactive.

Early Foundations (Elementary School)

The journey begins with whole numbers, fractions and mixed numbers, and decimals. Students also learn basic operations with ratio and proportion and how to express quantities using percent. Although formal algebra is not taught yet, these concepts are essential building blocks. At this stage, an algebra calculator can help learners visualize number relationships and practice converting between fractions, decimals, and percentages.

Introduction to Algebra (Middle School)

Around grades 7–8, students are introduced to variables, simple equations, and inequalities. They start learning to simplify expressions, apply scientific notation, and understand the meaning of unknown values. This stage often culminates in a pre-algebra or introductory algebra course. Using an AI Homework Helper alongside an algebra calculator makes it easier to grasp these abstract ideas.

Algebra 1 and Beyond (High School)

In high school, Algebra 1 becomes a cornerstone subject. Students work with polynomials, exponent and radicals, and the basics of rational functions. They also study how to determine the domain and range of different functions, which is critical for advanced math. Later, Algebra 2 expands on these topics and introduces more complex problem-solving. Practicing with an algebra calculator at this level helps students verify solutions and prepare for standardized tests like the SAT and ACT.

Advanced Applications (College and Beyond)

At the college level, algebra supports fields such as engineering, computer science, and economics. Students apply algebra in modeling, data analysis, and higher courses like calculus and linear algebra. Concepts like modulo operations and abstract algebra appear here. A strong background built along the learning path, reinforced with a Math AI tool, ensures students can transition smoothly into advanced applications.

Step-by-Step Calculations: Equations, Fractions, Parabolas

Calculating algebraic expressions is easier when you follow a clear sequence: identify the structure, apply operations, and confirm the result. Whether starting with Algebra 1 or advancing through a full algebra learning path, digital tools make practice more efficient. An algebra calculator is especially useful because it verifies steps, highlights errors, and helps students focus on understanding the reasoning rather than just the arithmetic.

The three worked examples below—a linear equation, a fraction operation, and a quadratic parabola—were chosen because they represent core milestones in algebra learning. Solving a linear equation introduces the idea of isolating a variable. Fraction operations bridge arithmetic with algebra, since fractions and mixed numbers often appear inside algebraic expressions. Finally, working with quadratics and parabolas showcases the leap from symbolic manipulation to function analysis, including concepts like domain and range.

Solving a Linear Equation

Consider the equation x+5=12.

Identify constants and variables: x is unknown, while 5 and 12 are constants.

Subtract 5 from both sides: x+5−5=12−5.

Simplify to get x=7.

Check by substitution: 7+5=12.

Practicing this process with an algebra calculator helps confirm the answer and makes solving more complex equations less intimidating.

Working with Fractions

Fractions appear often in algebra, so fluency is essential.

For instance, add $23\tfrac{2}{3}$ and $16\tfrac{1}{6}$.

First, rewrite with a common denominator of 6: $23\tfrac{2}{3} = 23\tfrac{4}{6}$ (since $\tfrac{2}{3} = \tfrac{4}{6}$).

Then add the whole numbers and fractions separately: whole numbers $23 + 16 = 39$, fractions $\tfrac{4}{6} + \tfrac{1}{6} = \tfrac{5}{6}$. Combine them to get $39\tfrac{5}{6}$.

The same strategy applies to fractions and mixed numbers, where converting to improper fractions makes calculations easier. An AI Math Calculator can show each step, guiding students to simplify correctly and avoid common mistakes.

Exploring a Parabola

Quadratic functions create parabolas, and solving them builds a bridge to higher algebra.

Take the equation $x^2 - 1 = 0$. Using the quadratic formula:

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Here $a=1$, $b=0$, and $c=-1$.

Substituting gives $x = \pm 1$.

Thus, the parabola $y = x^2$ has solutions at $x = -1$ and $x = 1$, with a domain of $(-\infty, \infty)$ and a range of $[0, \infty)$.

Exploring these graphs with a reliable Math AI tool reinforces connections between symbolic solutions and their geometric meaning.

By combining systematic steps with supportive tools, students gain clarity in solving equations, handling fractions, and interpreting quadratic graphs. An algebra calculator serves as both a practice partner and a learning aid, ensuring accuracy while strengthening long-term understanding.

Advanced Algebra Applications

As students progress beyond introductory algebra, they encounter more complex expressions involving exponents, radicals, ratios, and polynomials. These examples illustrate how an algebra calculator can support deeper learning by showing every step and preventing small mistakes from blocking conceptual understanding.

Exponents and Radicals

Exponents represent repeated multiplication, while radicals are their inverse, often involving square roots or higher roots. These operations are foundational for advanced algebra and scientific notation. For example, consider solving a simple radical equation:

$$\sqrt{x + 4} = 2$$

Eliminate the radical by squaring both sides :

$$(\sqrt{x + 4})^2 = 2^2$$

Simplifies to:

$$x + 4 = 4$$

Solve for $x$ by subtracting 4 from both sides:

$$x + 4 - 4 = 4 - 4$$

Yields:

$$x = 0$$

Verify the solution – substitute $x =0 $ back into the original equation:

$$\sqrt{0 + 4} = \sqrt{4} = 2$$

The left-hand side equals the right-hand side, so $x = 0$ is a valid solution.

Ratio and Proportion

Ratios compare two quantities, and proportions show when two ratios are equal. They are essential for solving practical problems in geometry, physics, and everyday life. For instance, to solve the proportion:

$$\frac{x}{3} = \frac{4}{6}$$

Simplify the known ratio (optional but helps reduce calculation):

$$\frac{4}{6}$$ simplifies to $\frac{2}{3}$, so the proportion becomes $\frac{x}{3} = \frac{2}{3}$; or directly use cross-multiplication:

For $\frac{x}{3} = \frac{4}{6}$, cross-multiply (multiply numerator of first ratio by denominator of second ratio, and vice versa):

$$x \times 6 = 3 \times 4$$

Simplifies to:

$$6x = 12$$

Solve for $x$ by dividing both sides by 6:

$$\frac{6x}{6} = \frac{12}{6}$$

Yields:

$$x = 2$$

Verify the solution – substitute $x =2 $ back into the original proportion to check if both ratios are equal:

Left-hand side: $\frac{2}{3}$; Right-hand side: $\frac{4}{6} = \frac{2}{3}$

Both sides are equal, so $x = 2$ is a valid solution.

Polynomial Simplification

Simplifying polynomials involves expanding, combining like terms, or factoring expressions. This process reduces complexity and prepares students for higher-level topics like rational functions and calculus. For example, consider:

$$(x + 2)(x - 3)$$

Expand using the distributive property (also called the FOIL method: First, Outer, Inner, Last terms):

• First: $$x \times x = x^2$$
• Outer: $$x \times (-3) = -3x$$
• Inner: $$2 \times x = 2x$$
• Last: $$2 \times (-3) = -6$$

Combining these terms gives:

$$x^2 - 3x + 2x - 6$$

Combine like terms (terms with the same variable raised to the same power);

$$x^2 + (-3x + 2x) - 6$$

Simplifies to:

$$x^2 - x - 6$$

Verify (by substituting a value for $x$ to check if expanded form equals simplified form) – let $x = 1$:

• Original expression: $$(1 + 2)(1 - 3) = 3 \times (-2) = -6$$
• Simplified form: $$1^2 - 1 - 6 = 1 - 1 - 6 = -6$$

Both results are equal, confirming the simplification is correct.

By combining these six worked examples—three foundational and three advanced—we create a balanced view of algebra skills. Together, they reflect the progressive challenges students encounter, from solving simple linear equations to simplifying polynomials. This progression highlights why an algebra calculator is not just a quick answer tool but also a reliable guide that reinforces accuracy, supports critical thinking, and strengthens the entire algebra learning path.

⚠Explore more math solutions today❗ Try GoMim Math Calculator

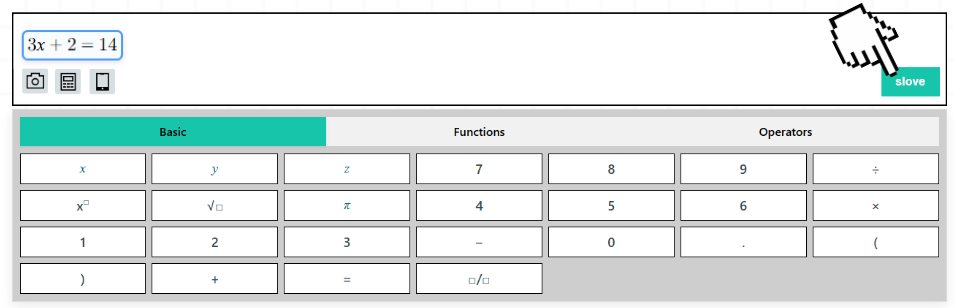
Related Practice Problem

Problem:

Solve for x in the linear equation 3x+2=14.

Step-by-Step Solution:

1、Isolate the variable term

Subtract 2 from both sides to eliminate the constant term on the left:

$$3x + 2 - 2 = 14 - 2$$

Simplifies to:

$$3x = 12$$

2、Solve for $x$

Divide both sides by 3 to isolate $x$:

$$\frac{3x}{3} = \frac{12}{3}$$

Simplifies to:

$$x =4 $$

3、Verify the solution

  Substitute $x = 4$ back into the original equation to check validity:

  Left-hand side: $$3(4) + 2 = 12 + 2 = 14$$

  Right-hand side: $$14$$

  Both sides are equal, confirming $x =4 $ is correct.

Using an algebra calculator can help students perform each step efficiently, check their work, and focus on understanding the reasoning behind solving linear equations.

Use GoMim for Algebra Practice

Tackling algebraic problems becomes much easier with the GoMim Math AI Solver. This intelligent tool allows you to input equations—whether linear, quadratic, or more advanced polynomial and exponential expressions—and instantly receive step-by-step solutions. Beyond just giving answers, it helps students understand the reasoning behind each step, making it an excellent algebra calculator for practice and homework. By exploring solutions interactively, learners can strengthen their understanding of concepts like fractions and mixed numbers, exponents and radicals, and domain and range. Try GoMim today and experience the convenience of solving math problems with a powerful AI Math Solver.

Conclusion

Algebra is a cornerstone of mathematics, connecting basic arithmetic to advanced topics and real-world applications. Mastering algebra enhances problem-solving skills and prepares students for higher studies in mathematics, science, engineering, and economics. Tools like the GoMim Math AI Solver make algebra more approachable, combining the benefits of an AI Homework Helper, AI Math Calculator, and interactive learning aid. By embracing these technologies, learners can simplify complex equations, explore concepts like fractions, exponents, and polynomials, and build confidence in their mathematical journey. Start using GoMim today to make algebra practice efficient, accurate, and engaging.

FAQ

Q: What is algebra used for?

A: Algebra is used to solve equations, model real-world situations, and provide a foundation for advanced studies in mathematics, science, and engineering.

Q: How do you solve algebraic equations?

A: Algebraic equations are solved by isolating the variable, simplifying the expressions, and verifying the solution for accuracy. Using an algebra calculator can make these steps more efficient.

Q: What are variables in algebra?

A: Variables are symbols, usually letters, that represent unknown values in equations or expressions, allowing for generalization and systematic problem-solving.

Q: Can algebra be solved using AI tools?

A: Yes, AI tools like the GoMim Math AI Solver provide step-by-step solutions, guiding learners through both simple and complex algebraic problems.

Q: Is algebra necessary for calculus?

A: Absolutely. Algebra provides the fundamental skills for understanding functions, derivatives, integrals, and other calculus concepts.

Q: How do algebra calculators help?

A: Algebra calculators show each calculation step, verify results, and help students understand concepts like polynomials, ratios and proportions, and radicals. They turn practice into active learning rather than memorization.

Related Topics

• Literal Equations Calculator
• Point Slope Form
• Midpoint formula
• Adding Exponents
• Rational numbers
• Irrational numbers
• Recursive Formula
• Natural Numbers
• Roman numerals
• Place value chart