GoMim AI |Learn Unit Circle: Chart, Steps, Tips

The unit circle is essential in trigonometry, helping connect angles with sine, cosine, and tangent. Using a unit circle chart, students can visualize these relationships clearly. With GoMim's AI Math Calculator, learners can grasp unit circle and explore step-by-step solutions, making math AI tools practical for mastering concepts efficiently.

Definition of the Unit Circle

The unit circle is a special circle in mathematics with a radius of one unit, centered at the origin of the cartesian coordinates system. Its equation is written as $x^2 + y^2 = 1$

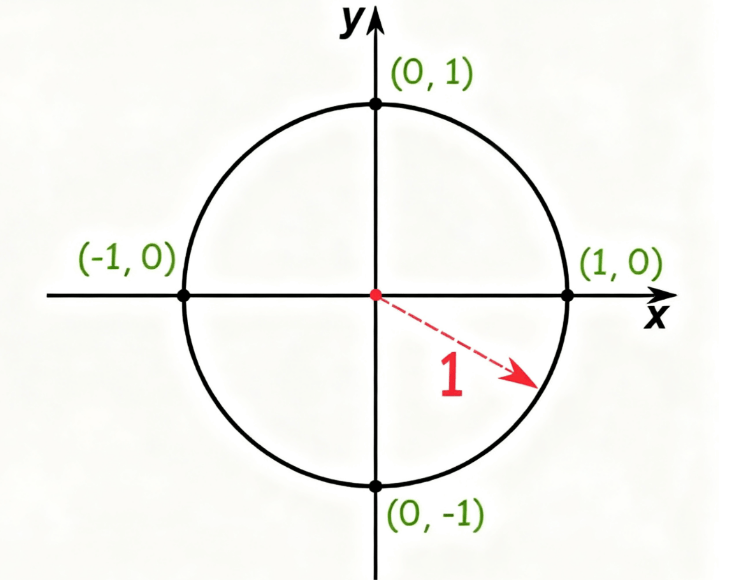
This simple yet powerful formula means that every point (x,y)lying on the circle satisfies the relationship defined by Pythagoras' theorem. Because of its fixed radius, the unit circle provides a universal model for exploring trigonometry, where each angle corresponds to a point on the circle. By using a unit circle chart, students and educators can easily connect the angle measure with the coordinates, which later translate into values of sine, cosine, and tangent. This connection makes the unit circle one of the most effective tools for both learning and applying trigonometric concepts.

Importance of the Unit Circle

The unit circle is essential in trigonometry because it connects angles with coordinates in the cartesian system, making abstract ideas easier to visualize. Every angle corresponds to a point on the circle, where the x-coordinate represents cosine and the y-coordinate represents sine.

For example, the point $\left(\tfrac{\sqrt{3}}{2}, \tfrac{1}{2}\right)$ on the unit circle chart shows the exact values for a $30^\circ$ angle without using a calculator.

Understanding the four quadrants also helps determine the signs of sine and cosine. For instance, in the second quadrant, sine is positive while cosine is negative. This rule simplifies working with trigonometric identities and graphs. In addition, mastering angle conversion from degrees to radians, such as $120^\circ = \tfrac{2\pi}{3}$, is critical for solving equations in advanced mathematics, physics, and engineering.

Unit Circle and Trigonometric Identities

The unit circle is not only a geometric figure but also the foundation of trigonometric identities. It is defined by the equation

$$x^2 + y^2 = 1$$

Now, consider an angle $\theta$ measured from the positive $x$-axis. If we draw the terminal side of this angle until it intersects the unit circle, the intersection point has coordinates $(x, y)$.

From basic right-triangle trigonometry:

• In a right triangle, $\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}$, and $\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}$.
• On the unit circle, the hypotenuse is the radius, which equals 1.
• Therefore, $\cos \theta = \frac{x}{1} = x$, and $\sin \theta = \frac{y}{1} = y$.

This shows why the coordinates of any point on the unit circle can be expressed as

$$(x, y) = (\cos \theta, \sin \theta)$$

With this definition, the equation of the unit circle becomes

$$\cos^2 \theta + \sin^2 \theta =1 $$

which is exactly the Pythagorean identity in trigonometry.

Moreover, the tangent function follows naturally as

$$\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{y}{x}$$

whenever $x \neq 0$.

This connection explains why the unit circle chart is such a powerful tool: it transforms triangle ratios into simple coordinates on a circle.

For solving problems, it is also necessary to switch between degrees and radians, since both are common in mathematics and physics.

Angle Conversion Between Degrees and Radians

The conversion rule is $$\text{radians} = \text{degrees} \times \frac{\pi}{180}$$

Some essential conversions include:

• $0^\circ = 0$ radians
• $30^\circ = \tfrac{\pi}{6}$
• $45^\circ = \tfrac{\pi}{4}$
• $60^\circ = \tfrac{\pi}{3}$
• $90^\circ = \tfrac{\pi}{2}$

By practicing with these values on the unit circle, students can quickly recall exact results for sine, cosine, and tangent, building both accuracy and fluency in trigonometric problem-solving.

Unit Circle Chart: Visualizing Key Angles and Values

To make these ideas clearer, a unit circle chart gives a visual summary of all the key angles, their radian measures, and corresponding coordinates. The chart you see above illustrates how each angle corresponds to a point on the circle, making it much easier to understand why $x = \cos \theta$ and $y = \sin \theta$.

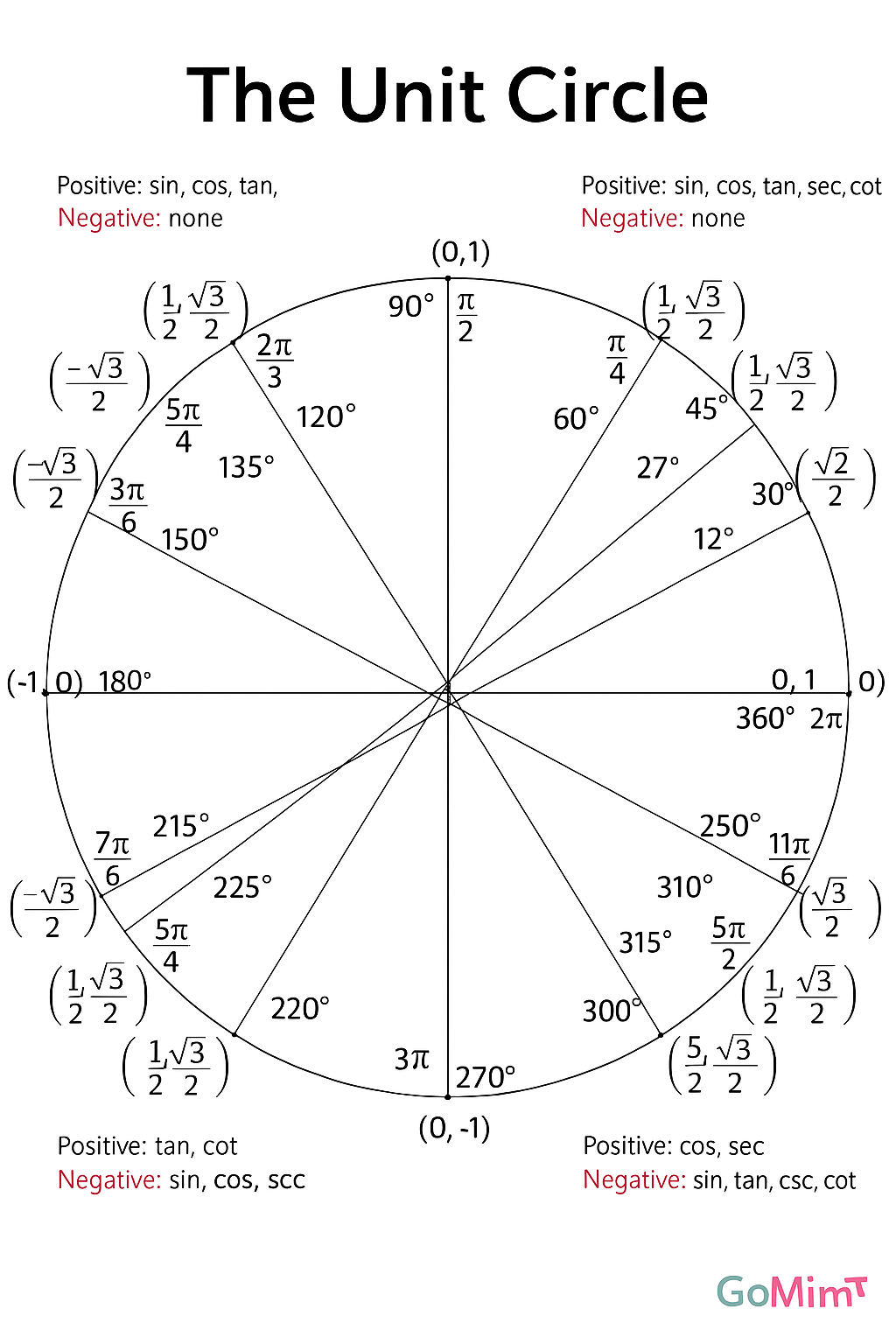
Take a look at the special angles shown in the diagram. At 30° ($\tfrac{\pi}{6}$), the coordinates are $\left(\tfrac{\sqrt{3}}{2}, \tfrac{1}{2}\right)$, so we read directly that $\cos 30^\circ = \tfrac{\sqrt{3}}{2}$ and $\sin 30^\circ = \tfrac{1}{2}$. At 45°($\tfrac{\pi}{4}$), both coordinates are $\tfrac{\sqrt{2}}{2}$, which connects neatly to the symmetry of an isosceles right triangle. By using the chart, learners can not only memorize these values but also visualize why they are true.

The chart also helps with quadrant rules. For example, in the second quadrant, sine values are positive while cosine values are negative. This is immediately visible in the coordinates and helps when applying identities or graphing trigonometric functions.

Finally, the chart reinforces the idea of degree–radian conversion. A full circle is both 360° and 2Π radians, and the diagram highlights common benchmarks like $90^\circ = \tfrac{\pi}{2}$, $180^\circ = \pi$, and $270^\circ = \tfrac{3\pi}{2}$. With practice, these conversions become second nature, speeding up problem solving in mathematics, physics, and engineering.

Special Angles and Memory Tricks

In trigonometry, certain angles appear so often that knowing their exact values is a huge advantage. On the unit circle chart, the most common special angles are $$0^\circ, 30^\circ, 45^\circ, 60^\circ, \text{and } 90^\circ$$

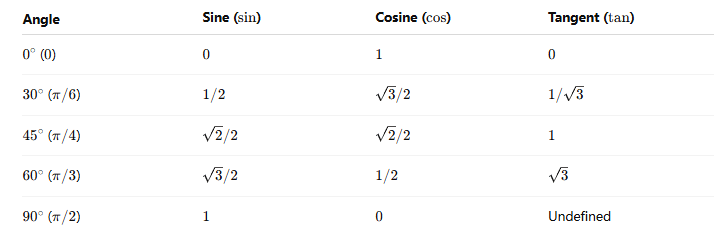
Memory Tips

• Finger Trick:

1、Spread out your left hand, and let each finger represent a special angle:

• Thumb = 0°
• Index finger =30°
• Middle finger = 45°
• Ring finger = 60°
• Pinky finger = 90°

2、Value Calculation Rules:

• Sine of the angle: $\sin \theta = \frac{\sqrt{\text{number of fingers below the target finger}}}{2}$
• Cosine of the angle: $\cos \theta = \frac{\sqrt{\text{number of fingers above the target finger}}}{2}$
• Tangent of the angle: $\tan \theta = \frac{\sqrt{\text{number of fingers below the target finger}}}{\sqrt{\text{number of fingers above the target finger}}}$

3、Example (for $30^\circ$):

• Target finger for $30^\circ$: Index finger
• Number of fingers below: 1 (only the thumb)$\sin 30^\circ = \frac{\sqrt{1}}{2} = \frac{1}{2}$
• Number of fingers above: 3 (middle, ring, pinky fingers)$\cos 30^\circ = \frac{\sqrt{3}}{2}$
• Thus, $\tan 30^\circ = \frac{1}{\sqrt{3}}$
• Symmetry Tip: Notice that $\sin 30^\circ = \cos 60^\circ$ and $\sin 60^\circ = \cos 30^\circ$—sine and cosine swap values between $30^\circ$ and $60^\circ$. This symmetry reduces the need for extra memorization.

Step-by-Step Problem Solving with the Unit Circle

Now that you are comfortable with the unit circle and the unit circle chart, here is a clear, repeatable step-by-step method you can use to solve trigonometric problems and check your work.

Step 1 — Read and isolate

Read the problem and isolate the trigonometric expression. Example:

$\sin \theta = \tfrac{1}{2}$ or $\cos \theta = -\tfrac{\sqrt{2}}{2}$.

Step 2 — Make sure units match

Decide whether the problem uses degrees or radians. If you need to convert, use

$$\text{radians} = \text{degrees} \times \frac{\pi}{180}$$

Convert the given values if necessary, so you can read them from the unit circle chart.

Step 3 — Find the reference angle

Use the unit circle chart to find the acute reference angle $\alpha$ that gives the absolute value of the function.

• For $\sin \theta = \tfrac{1}{2}$, the reference angle is $\alpha = \tfrac{\pi}{6}$ because the chart shows $\sin\left(\tfrac{\pi}{6}\right) = \tfrac{1}{2}$.
• For $\cos \theta = -\tfrac{\sqrt{2}}{2}$, the reference angle is $\alpha = \tfrac{\pi}{4}$ because $\cos\left(\tfrac{\pi}{4}\right) = \tfrac{\sqrt{2}}{2}$ (sign to be determined by quadrant).

Step 4 — Determine correct quadrants by sign

Use quadrant rules (visible on the unit circle chart):

• Sine positive in quadrants I and II.
• Cosine positive in quadrants I and IV.
• Tangent sign follows from $\tan \theta = \dfrac{\sin \theta}{\cos \theta}$.

Example: $\sin \theta = \tfrac{1}{2}$ is positive, so solutions in $[0, 2\pi$ lie in quadrants I and II.

Step 5 — Write the principal solutions (on $[0, 2\pi)$)

Place the reference angle into the correct quadrants:

• For $\sin \theta = \tfrac{1}{2}$:$\theta = \tfrac{\pi}{6}, \quad \theta = \pi - \tfrac{\pi}{6} = \tfrac{5\pi}{6}$.
• For $\cos \theta = -\tfrac{\sqrt{2}}{2}$ (quadrants II and III):$\theta = \pi - \tfrac{\pi}{4} = \tfrac{3\pi}{4}, \quad \theta = \pi + \tfrac{\pi}{4} = \tfrac{5\pi}{4}$.

Step 6 — Write the general solution

Add full rotations $2\pi $ (where $n$ is any integer) to cover all solutions:

$$\theta = \tfrac{\pi}{6} + 2n\pi, \quad \theta = \tfrac{5\pi}{6} + 2n\pi, \quad n \in \mathbb{Z}$$

Step 7 — Verify with identities or coordinates

Check results by substituting into the unit circle's coordinate definition $(\cos \theta, \sin \theta)$, or by using the Pythagorean identity:

$$\sin^2 \theta + \cos^2 \theta = 1$$

For instance, if $\cos \theta = \tfrac{1}{2}$, then $\sin \theta = \pm \sqrt{1 - \left(\tfrac{1}{2}\right)^2} = \pm \tfrac{\sqrt{3}}{2}$; pick the sign based on the quadrant.

Step 8 — Optional: use an AI Math Solver for a quick check

If you want a step-by-step verification or a diagram that highlights the angles on a unit circle chart, try an AI Math Solver or AI Math Calculator such as GoMim to confirm your steps and see a visual check.

Use this routine every time you tackle a trig equation. With practice the steps become automatic: isolate, convert units, find the reference angle on the unit circle chart, pick quadrants by sign, list principal solutions, extend with $2\pi n$, and verify.

Related Practice Problem-Unit Circle Coordinates

Problem: Finding Coordinates on the Unit Circle for 120°

Find the coordinates of the point on the unit circle at an angle of $120^\circ$.

Solution:

• Step 1 — Convert the angle to radians

Since many formulas and the unit circle chart use radians, convert $120^\circ$ to radians:

$120^\circ \times \frac{\pi}{180} = \frac{2\pi}{3} \text{ radians}$

• Step 2 — Identify the quadrant

From the unit circle chart:

- $120^\circ$ lies in the second quadrant.

- In quadrant II, sine is positive and cosine is negative.

• Step 3 — Determine the reference angle

The reference angle $\alpha$ is the acute angle formed with the $x$-axis:

$\alpha = 180^\circ - 120^\circ = 60^\circ \quad \text{or} \quad \alpha = \pi - \frac{2\pi}{3} = \frac{\pi}{3}$

• Step 4 — Use sine and cosine values for the reference angle

From the unit circle chart for $60^\circ = \frac{\pi}{3}$:

$\cos \alpha = \frac{1}{2}, \quad \sin \alpha = \frac{\sqrt{3}}{2}$

• Step 5 — Apply quadrant signs

Adjust the signs according to quadrant II (cosine negative, sine positive):

$x = \cos 120^\circ = -\frac{1}{2}, \quad y = \sin 120^\circ = \frac{\sqrt{3}}{2}$

• Step 6 — Verify the point lies on the unit circle

Check using the Pythagorean identity $x^2 + y^2 = 1$:

$\left(-\frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2 = \frac{1}{4} + \frac{3}{4} = 1$

Answer:

The coordinates of the point are:

$\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$

Step 7 — Optional:

Use GoMim's AI Math Calculator to visualize the point in the unit circle and check your work step-by-step.

⚠Explore more math solutions today❗ Try GoMim Math Calculator

Use GoMim Math AI Solver to Master the Unit Circle

Still struggling with unit circle angles and calculating sine, cosine, or tangent values? With the GoMim Math AI Solver, mastering trigonometry has never been easier. Simply enter an angle in degrees or radians, and the tool provides instant and accurate values along with a detailed step-by-step explanation. By referencing the unit circle chart, you can visualize how each angle corresponds to a point in cartesian coordinates and determine the correct quadrant signs. Whether you are preparing for exams or tackling challenging homework problems, GoMim acts as an AI Homework Helper and AI Math Calculator, guiding your learning and reinforcing your understanding of trigonometric concepts.

Try GoMim now and experience how Math AI can simplify your study of the unit circle, one angle at a time.

Conclusion

The unit circle is essential for understanding trigonometry, linking angles in degrees or radians to sine, cosine, and tangent values. Using a unit circle chart, students can see how each angle corresponds to a point in cartesian coordinates and determine the correct quadrant. Mastery of the unit circle builds a strong foundation for advanced math, physics, and engineering. With GoMim AI Math Calculator and other Math AI tools, learners can explore step-by-step solutions, verify their work, and approach problems with confidence.

Frequently Asked Questions

Q: What is the unit circle?

A circle with radius 1 in cartesian coordinates, linking angles in degrees or radians to sine, cosine, and tangent using a unit circle chart.

Q: How do I read sine, cosine, and tangent?

Use the unit circle chart: x = cosine, y = sine, and tangent = y/x, adjusting signs by quadrant.

Q: Can GoMim help with unit circle problems?

Yes, GoMim acts as an AI Math Solver and AI Math Calculator, giving step-by-step solutions and visualizing points on the unit circle chart.

Q: Why are special angles important?

Angles like 30°, 45°, and 60° appear often in trigonometry, and their values are easy to read and memorize using the unit circle chart.

Q: How can I check my unit circle work?

Verify coordinates with Pythagoras' theorem or use GoMim Math AI Calculator for step-by-step validation and visualization.